The Problem with How We Teach Math
Why do some children find Math hard to learn? I suspect that this is often caused by starting with the practice and drill of a bunch of skills called Arithmetic—and instead of promoting inventiveness, we focus on preventing mistakes. I suspect that this negative emphasis leads many children not only to dislike Arithmetic, but also later to become averse to everything else that smells of technology. It might even lead to a long-term distaste for the use of symbolic representations.
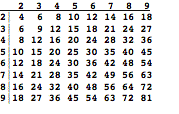
Anecdote: A parent once asked me to tutor a student who was failing to learn the multiplication table. When the child complained that this was a big job, I tried to explain that because of diagonal symmetry, there are less than 50 facts to learn.

½
However, that child had a larger-scale complaint:
“Last year I had to learn the addition table and it was really boring. This year I have to learn another, harder one, and I figure if I learn it then next year there will be another one and there’ll never be any end to this stupid nonsense. "
This child imagined ‘Math’ to be a continuous string of mechanical tasks—an unending prospect of practice and drill. It was hard to convince him that there would not be any more tables in subsequent years.
To deal with the immediate problem, I made a deck of “flash cards,” each of which showed two digits on the front and their product on the back. The process was to guess each answer and, if it was correct, then to remove that card from the deck. This made the task seem more like a game in which one can literally feel one’s progress as the size and weight of the deck diminishes. Shortly the child excitedly said, “This deck is a really smart teaching machine! It remembers which products I’ve learned, and then only asks for the ones I don’t know, so it saves me from wasting a lot of time!”
However, a more serious problem was that this child had no good image or “cognitive map” of what might result from learning this subject. What function might Math serve in later years? What goals and ambitions might it help to achieve?
Anecdote: I asked a certain 6-year-old child “how much is 15 and 15”and she quickly answered, “I think it’s 30.” I asked how she figured that out so fast and she replied, “Well, everyone knows that 16 and 16 is 32, so then I subtracted the extra two 1’s.”
Traditional teacher: “Your answer is right but your method was wrong: you should add the two 5’s to make a 10; then write down the 0 and carry the 1, and then add it to the other two 1’s.”
The traditional emphasis on accuracy leads to weakness of ability to make order-of-magnitude estimates—whereas this particular child already knew and could use enough powers of 2 to make approximations that rivaled some adult’s abilities. Why should children learn only “fixed-point” arithmetic, when “floating point” thinking is usually better for problems of everyday life!
More generally, we need to develop better ways to answer the questions that kids are afraid to ask, like “What am I doing here, and why? ”What can I expect to happen next?” or “Where and when could I find any use for this?
I’ll conclude with a perceptive remark from MIT’s Phil Sung: “Students are being led to think that they dislike math when they actually just dislike whatever it is that they're being taught in math classes.”
Notes:
Folksonomies: education mathematics
Taxonomies:
/business and industrial/construction (0.574672)
/sports/table tennis and ping-pong (0.569772)
/health and fitness/disorders/mental disorder/a.d.d. (0.519545)
Keywords:
certain 6-year-old child (0.929268 (neutral:0.000000)), smart teaching machine (0.917502 (positive:0.646084)), diagonal symmetry (0.780648 (negative:-0.616258)), larger-scale complaint (0.779674 (negative:-0.501919)), multiplication table. (0.774697 (negative:-0.488946)), symbolic representations (0.769854 (negative:-0.687634)), big job (0.769546 (negative:-0.488946)), long-term distaste (0.767468 (negative:-0.687634)), unending prospect (0.761859 (neutral:0.000000)), stupid nonsense (0.758851 (negative:-0.763660)), negative emphasis (0.758573 (negative:-0.763240)), addition table (0.751852 (negative:-0.814117)), mechanical tasks—an (0.743504 (neutral:0.000000)), perceptive remark (0.742983 (positive:0.608674)), flash cards (0.740522 (neutral:0.000000)), continuous string (0.732598 (neutral:0.000000)), immediate problem (0.729901 (neutral:0.000000)), good image (0.729760 (negative:-0.529530)), cognitive map (0.724593 (negative:-0.314623)), better ways (0.721777 (negative:-0.442272)), Phil Sung (0.720227 (positive:0.608674)), particular child (0.719791 (negative:-0.338744)), order-of-magnitude estimates—whereas (0.719535 (negative:-0.338744)), adult’s abilities. (0.718760 (negative:-0.338744)), Traditional teacher (0.717629 (positive:0.423612)), math classes (0.717209 (neutral:0.000000)), everyday life (0.713408 (neutral:0.000000)), traditional emphasis (0.704409 (negative:-0.338744)), deck (0.695641 (positive:0.164647)), children (0.636859 (negative:-0.582679))
Entities:
two digits:Quantity (0.010000 (neutral:0.000000)), 6-year:Quantity (0.010000 (neutral:0.000000))
Concepts:
Question (0.920705): dbpedia | freebase
Pleading (0.873734): dbpedia | freebase
Learning (0.776294): dbpedia | freebase | opencyc
Psychology (0.641344): dbpedia | freebase | opencyc
Mathematics (0.613123): dbpedia | freebase | opencyc
Child (0.610156): dbpedia | freebase | opencyc
Knowledge (0.605243): dbpedia | freebase
Elementary arithmetic (0.599695): dbpedia | freebase




